Materi Soal dan Pembahasan Sudut Pusat dan Sudut Keliling Lengkap
Ini adalah pembahasan lengkap tentang hubungan antara sudut pusat dan sudut keliling di dalam lingkaran.
Salah satu materi yang penting untuk kita ketahui tentang lingkaran adalah hubungan sudut - sudut di dalamnya.
Dua diantaranya adalah sudut pusat dan sudut keliling.
Pada gambar di atas $\angle \ AOB$ merupakan sebuah sudut pusat yang menghadap busur $AB$ dimana $OB=OA$ adalah jari - jari lingkaran tersebut.
Pada gambar di atas $\angle \ FDE$ adalah sebuah sudut keliling yang menghadap busur $EF$ dengan $DF$ dan $DE$ masing - masing merupakan tali busur pada lingkaran tersebut.
Pada gambar di atas terlihat jelas bahwa $\angle \ AOB$ ialah sudut pusat lingkaran dan $\angle \ ACB$ merupakan sudut keliling lingkaran.
Karena $\angle \ AOB$ dan $\angle \ ACB$ sama - sama menghadap busur $AB$ maka berlaku :
$\angle \ AOB=2 \times \angle \ ACB$
Ternyata mencari sudut pusat dan sudut keliling pada lingkaran itu mudah bukan.
Perbanyak latihan dengan bentuk soal - soal yang lain agar kalian makin paham dan jago lagi.
Dua diantaranya adalah sudut pusat dan sudut keliling.
A. Sudut Pusat Lingkaran
Sudut pusat lingkaran adalah sebuah sudut yang menghadap busur lingkaran dimana sudut tersebut diapit oleh kedua jari - jari lingkaran dan titik pusatnya.
B. Sudut Keliling Lingkaran
Sudut keliling lingkaran adalah sebuah sudut yang dibentuk oleh dua buah tali busur dengan sebuah titik pada tepi sebuah lingkaran.
C. Hubungan Sudut Pusat dan Sudut Keliling Lingkaran
Jika terdapat sebuah sudut pusat dan sudut keliling masing - masing menghadap busur lingkaran yang sama maka akan berlaku sudut pusat sama dengan dua kali sudut kelilingnya.
Karena $\angle \ AOB$ dan $\angle \ ACB$ sama - sama menghadap busur $AB$ maka berlaku :
$\angle \ AOB=2 \times \angle \ ACB$
D. Contoh Soal Sudut Pusat dan Sudut Keliling
Nah di bawah ini ada beberapa contoh yang bisa buat bahan belajar kalian agar makin paham dengan apa yang kita bahas kali ini.
Contoh Soal 1
Perhatikan gambar di bawah ini !
Jika $\angle \ POR=85^{\circ}$ maka besar $\angle \ PQR$ adalah ...
$ \begin{align} & (A) \ 42,5^{\circ} \\ & (B) \ 65,5^{\circ} \\ & (C) \ 150^{\circ} \\ & (D) \ 170^{\circ} \end{align} $
Perhatikan gambar di bawah ini !
$ \begin{align} & (A) \ 42,5^{\circ} \\ & (B) \ 65,5^{\circ} \\ & (C) \ 150^{\circ} \\ & (D) \ 170^{\circ} \end{align} $
Karena $\angle \ PQR$ dan $\angle \ POR$ sama - sama menghadap busur $PR$ maka,
$ \begin{align} \angle \ POR &= 2 \times \angle \ PQR \\ 85^{\circ} &= 2 \times \angle \ PQR \\ \dfrac{1}{2} \times 85^{\circ} &= \angle \ PQR \\ 42,5^{\circ} &= \angle \ PQR \end{align} $
Jadi pilihan jawaban yang BENAR adalah $(A) \ 42,5^{\circ}$.
$ \begin{align} \angle \ POR &= 2 \times \angle \ PQR \\ 85^{\circ} &= 2 \times \angle \ PQR \\ \dfrac{1}{2} \times 85^{\circ} &= \angle \ PQR \\ 42,5^{\circ} &= \angle \ PQR \end{align} $
Jadi pilihan jawaban yang BENAR adalah $(A) \ 42,5^{\circ}$.
Contoh Soal 2
Perhatikan gambar di bawah ini !
Jika besar $\angle \ BOC=100^{\circ}$ maka besar $\angle \ OAC$ adalah ...
$ \begin{align} & (A) \ 25^{\circ} \\ & (B) \ 50^{\circ} \\ & (C) \ 75^{\circ} \\ & (D) \ 80^{\circ} \end{align} $
Perhatikan gambar di bawah ini !
$ \begin{align} & (A) \ 25^{\circ} \\ & (B) \ 50^{\circ} \\ & (C) \ 75^{\circ} \\ & (D) \ 80^{\circ} \end{align} $
Jika kita perhatikan dengan cermat, terlihat jelas bahwa $\angle \ OAC=\angle \ BAC$. Sementara $\angle \ BAC$ dan $\angle \ BOC$ sama - sama menghadap busur $BC$ sehingga,
$ \begin{align} \angle \ BOC &= 2 \times \angle \ BAC \\ 100^{\circ} &= 2 \times \angle \ OAC \\ \dfrac{1}{2} \times 100^{\circ} &= \angle \ OAC \\ 50^{\circ} &= \angle \ OAC \\ \end{align} $
Jadi pilihan jawaban yang BENAR adalah $(B) \ 50^{\circ}$.
$ \begin{align} \angle \ BOC &= 2 \times \angle \ BAC \\ 100^{\circ} &= 2 \times \angle \ OAC \\ \dfrac{1}{2} \times 100^{\circ} &= \angle \ OAC \\ 50^{\circ} &= \angle \ OAC \\ \end{align} $
Jadi pilihan jawaban yang BENAR adalah $(B) \ 50^{\circ}$.
Contoh Soal 3
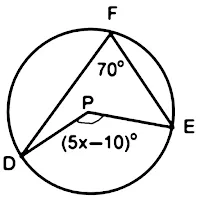
Perhatikan gambar di bawah ini !
Jika besar nilai $x$ adalah ...
$ \begin{align} & (A) \ 9 \\ & (B) \ 16 \\ & (C) \ 30 \\ & (D) \ 44 \end{align} $
Perhatikan gambar di bawah ini !
$ \begin{align} & (A) \ 9 \\ & (B) \ 16 \\ & (C) \ 30 \\ & (D) \ 44 \end{align} $
$
\begin{align}
\angle \ DPE &= 2 \times \angle \ DFE \\
(5x-10)^{\circ} &= 2 \times 70^{\circ} \\
5x-10 &= 140 \\
5x &= 150 \\
x &= 30
\end{align}
$
Jadi pilihan jawaban yang BENAR adalah $(C) \ 30 $.
Jadi pilihan jawaban yang BENAR adalah $(C) \ 30 $.
Contoh Soal 4
Perhatikan gambar di bawah ini !
Jika besar nilai $x$ adalah ...
$ \begin{align} & (A) \ 24 \\ & (B) \ 33 \\ & (C) \ 42 \\ & (D) \ 64 \end{align} $
Perhatikan gambar di bawah ini !
$ \begin{align} & (A) \ 24 \\ & (B) \ 33 \\ & (C) \ 42 \\ & (D) \ 64 \end{align} $
$
\begin{align}
\angle \ AOC &= 2 \times \angle \ ABC \\
(4x-12)^{\circ} &= 2 \times 60^{\circ} \\
4x-12 &= 120 \\
4x &= 132 \\
x &= 33
\end{align}
$
Jadi pilihan jawaban yang BENAR adalah $(B) \ 33 $.
Jadi pilihan jawaban yang BENAR adalah $(B) \ 33 $.
Contoh Soal 5
Perhatikan gambar di bawah ini !
Bila diketahui $\angle \ APB+\angle \ AQB+\angle \ ARB=144^{\circ}$, maka besar $\angle \ AOB$ adalah ...
$ \begin{align} & (A) \ 144^{\circ} \\ & (B) \ 96^{\circ} \\ & (C) \ 48^{\circ} \\ & (D) \ 24^{\circ} \end{align} $
Perhatikan gambar di bawah ini !
$ \begin{align} & (A) \ 144^{\circ} \\ & (B) \ 96^{\circ} \\ & (C) \ 48^{\circ} \\ & (D) \ 24^{\circ} \end{align} $
Pada gambar $\angle \ APB=\angle \ AQB=\angle \ ARB$ karena ketiganya sama - sama menghadap busur yang sama yaitu $AB$ dan merupakan sudut keliling.
Sedangkan sudut $\angle \ AOB$ adalah sudut pusat.
Misal $\angle \ APB=x$ maka :
$ \begin{align} \angle \ APB+\angle \ AQB+\angle \ ARB &= 144^{\circ} \\ x+x+x &= 144^{\circ} \\ 3x &= 144^{\circ} \\ x &= 48^{\circ} \end{align} $
Dengan demikian,
$ \begin{align} \angle \ AOB &= 2 \times \angle \ APB \\ &= 2 \times x \\ &= 2 \times 48^{\circ} \\ &= 96^{\circ} \end{align} $
Jadi pilihan jawaban yang BENAR adalah $(B) \ 96^{\circ} $.
Sedangkan sudut $\angle \ AOB$ adalah sudut pusat.
Misal $\angle \ APB=x$ maka :
$ \begin{align} \angle \ APB+\angle \ AQB+\angle \ ARB &= 144^{\circ} \\ x+x+x &= 144^{\circ} \\ 3x &= 144^{\circ} \\ x &= 48^{\circ} \end{align} $
Dengan demikian,
$ \begin{align} \angle \ AOB &= 2 \times \angle \ APB \\ &= 2 \times x \\ &= 2 \times 48^{\circ} \\ &= 96^{\circ} \end{align} $
Jadi pilihan jawaban yang BENAR adalah $(B) \ 96^{\circ} $.
Contoh Soal 6
Perhatikan gambar berikut !
Diketahui $O$ adalah titik pusat lingkaran. Besar sudut $ \angle \ AOB$ adalah ...
$ \begin{align} & (A) \ 15^{\circ} \\ & (B) \ 30^{\circ} \\ & (C) \ 60^{\circ} \\ & (D) \ 80^{\circ} \end{align} $
Perhatikan gambar berikut !
$ \begin{align} & (A) \ 15^{\circ} \\ & (B) \ 30^{\circ} \\ & (C) \ 60^{\circ} \\ & (D) \ 80^{\circ} \end{align} $
$
\begin{align}
\angle \ AOB &= 2 \times \angle \ ACB \\
&= 2 \times 40^{\circ} \\
&= 80^{\circ}
\end{align}
$
Jadi pilihan jawaban yang BENAR adalah $ (D) \ 80^{\circ}$.
Jadi pilihan jawaban yang BENAR adalah $ (D) \ 80^{\circ}$.
Contoh Soal 7
Perhatikan gambar berikut !
Diketahui $ \angle \ CDO=41^{\circ}$ dan $ \angle \ CBO=27^{\circ}$. Besar $ \angle \ AOD$ adalah ...
$ \begin{align} & (A) \ 72^{\circ} \\ & (B) \ 68^{\circ} \\ & (C) \ 56^{\circ} \\ & (D) \ 44^{\circ} \end{align} $
Perhatikan gambar berikut !
$ \begin{align} & (A) \ 72^{\circ} \\ & (B) \ 68^{\circ} \\ & (C) \ 56^{\circ} \\ & (D) \ 44^{\circ} \end{align} $
Untuk menjawab soal ini biar lebih mudah kita bisa pakai garis bantuan $OC$.
Sementara terlihat jelas bahwa $OB=OC=OD$ yang masing - masing merupakan jari - jari lingkarannya.
Sehingga akan terbentuk dua buah segitiga sama kaki yaitu $\triangle OCD$ dan $\triangle OBC$.
Dengan demikian,
$\clubsuit$
$ \begin{align} \angle DCO &= \angle CDO \\ \angle DCO &= 41^{\circ} \end{align} $
$\clubsuit$
$ \begin{align} \angle BCO &= \angle CBO \\ \angle BCO &= 27^{\circ} \end{align} $
$\clubsuit$
$ \begin{align} \angle BCD &= \angle DCO+\angle BCO \\ \angle BCD &= 41^{\circ}+27^{\circ}\\ \angle BCD &= 68^{\circ} \ \left( \text{sudut keliling} \right) \end{align} $
$\clubsuit$
$ \begin{align} \angle BOD &= 2 \times \angle BCD \\ \angle BOD &= 2 \times 68^{\circ} \\ \angle BOD &= 136^{\circ} \ \left( \text{sudut pusat} \right) \end{align} $
$\clubsuit$
$ \begin{align} \angle AOD &= 180^{\circ} - \angle BOD \\ &= 180^{\circ} - 136^{\circ} \\ &= 44^{\circ} \end{align} $
Jadi pilihan jawaban yang BENAR adalah $ (D) \ 44^{\circ}$.
Sementara terlihat jelas bahwa $OB=OC=OD$ yang masing - masing merupakan jari - jari lingkarannya.
Dengan demikian,
$\clubsuit$
$ \begin{align} \angle DCO &= \angle CDO \\ \angle DCO &= 41^{\circ} \end{align} $
$\clubsuit$
$ \begin{align} \angle BCO &= \angle CBO \\ \angle BCO &= 27^{\circ} \end{align} $
$\clubsuit$
$ \begin{align} \angle BCD &= \angle DCO+\angle BCO \\ \angle BCD &= 41^{\circ}+27^{\circ}\\ \angle BCD &= 68^{\circ} \ \left( \text{sudut keliling} \right) \end{align} $
$\clubsuit$
$ \begin{align} \angle BOD &= 2 \times \angle BCD \\ \angle BOD &= 2 \times 68^{\circ} \\ \angle BOD &= 136^{\circ} \ \left( \text{sudut pusat} \right) \end{align} $
$\clubsuit$
$ \begin{align} \angle AOD &= 180^{\circ} - \angle BOD \\ &= 180^{\circ} - 136^{\circ} \\ &= 44^{\circ} \end{align} $
Jadi pilihan jawaban yang BENAR adalah $ (D) \ 44^{\circ}$.
Contoh Soal 8
Perhatikan gambar lingkaran dengan pusat $O$ di bawah. Jika besar $ \angle \ AOD=80^{\circ}$, maka besar $ \angle \ ACB=$ ...
$
\begin{align}
& (A) \ 80^{\circ} \\
& (B) \ 50^{\circ} \\
& (C) \ 40^{\circ} \\
& (D) \ 35^{\circ}
\end{align}
$
Perhatikan gambar lingkaran dengan pusat $O$ di bawah. Jika besar $ \angle \ AOD=80^{\circ}$, maka besar $ \angle \ ACB=$ ...
$
\begin{align}
\angle \ AOD+\angle \ AOB &= 180^{\circ} \\
80^{\circ}+\angle \ AOB &= 180^{\circ} \\
\angle \ AOB &= 100^{\circ} \\
\end{align}
$
Sehingga,
$ \begin{align} \angle \ AOB &= 2 \times \angle \ ACB \\ \dfrac{1}{2} \times \angle \ AOB &= \angle \ ACB \\ \dfrac{1}{2} \times 100^{\circ} &= \angle \ ACB \\ \angle \ ACB &= 50^{\circ} \end{align} $
Jadi pilihan jawaban yang BENAR adalah $(B) \ 50^{\circ} $.
Sehingga,
$ \begin{align} \angle \ AOB &= 2 \times \angle \ ACB \\ \dfrac{1}{2} \times \angle \ AOB &= \angle \ ACB \\ \dfrac{1}{2} \times 100^{\circ} &= \angle \ ACB \\ \angle \ ACB &= 50^{\circ} \end{align} $
Jadi pilihan jawaban yang BENAR adalah $(B) \ 50^{\circ} $.
Contoh Soal 9
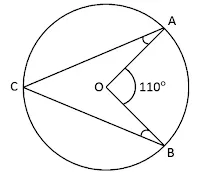
Perhatikan gambar lingkaran berikut!
Diketahui besar $\angle \ AOB=110^{\circ} $ maka besar $\angle \ OAC+\angle \ OBC+\angle \ ACB=$ ...
$ \begin{align} & (A) \ 27,5^{\circ} \\ & (B) \ 55^{\circ} \\ & (C) \ 110^{\circ} \\ & (D) \ 200^{\circ} \end{align} $
Perhatikan gambar lingkaran berikut!
$ \begin{align} & (A) \ 27,5^{\circ} \\ & (B) \ 55^{\circ} \\ & (C) \ 110^{\circ} \\ & (D) \ 200^{\circ} \end{align} $
Untuk menjawab soal ini perhatikan step by step berikut :
$ \begin{align} \angle AOB &= 2 \times \angle ACB \\ 110^{\circ} &= 2 \times \angle ACB \\ \angle ACB &= \dfrac{1}{2} \times 110^{\circ} \\ \angle ACB &= 55^{\circ} \end{align} $
Step berikutnya kita bisa pakai garis bantuan $AB$ sehingga akan terbentuk segitiga sama kaki $\triangle AOB$.
$
\begin{align}
\angle OBA &= \angle OAB \\
&= \left( \dfrac{180^{\circ}-110^{\circ}}{2} \right) \\
&= 35^{\circ}
\end{align}
$
$ \begin{align} \angle ABC &= \angle BAC \\ &= \left( \dfrac{180^{\circ}-\angle ACB}{2} \right) \\ &= \left( \dfrac{180^{\circ}-55^{\circ}}{2} \right) \\ &= 62,5^{\circ} \end{align} $
$ \begin{align} \angle ABC &= \angle OBC+\angle OBA \\ 62,5^{\circ} &= \angle OBC+35^{\circ} \\ \angle OBC &= 27,5^{\circ} \end{align} $
$ \begin{align} \angle BAC &= \angle OAC+\angle OAB \\ 62,5^{\circ} &= \angle OAC+35^{\circ} \\ \angle OAC &= 27,5^{\circ} \end{align} $
Sehingga,
$ \begin{align} &\angle OAC+\angle OBC+\angle ACB \\ &= 27,5^{\circ}+27,5^{\circ}+55^{\circ}\\ &= 110^{\circ} \end{align} $
Jadi pilihan jawaban yang BENAR adalah $(C) \ 110^{\circ} $.
$ \begin{align} \angle AOB &= 2 \times \angle ACB \\ 110^{\circ} &= 2 \times \angle ACB \\ \angle ACB &= \dfrac{1}{2} \times 110^{\circ} \\ \angle ACB &= 55^{\circ} \end{align} $
Step berikutnya kita bisa pakai garis bantuan $AB$ sehingga akan terbentuk segitiga sama kaki $\triangle AOB$.
$ \begin{align} \angle ABC &= \angle BAC \\ &= \left( \dfrac{180^{\circ}-\angle ACB}{2} \right) \\ &= \left( \dfrac{180^{\circ}-55^{\circ}}{2} \right) \\ &= 62,5^{\circ} \end{align} $
$ \begin{align} \angle ABC &= \angle OBC+\angle OBA \\ 62,5^{\circ} &= \angle OBC+35^{\circ} \\ \angle OBC &= 27,5^{\circ} \end{align} $
$ \begin{align} \angle BAC &= \angle OAC+\angle OAB \\ 62,5^{\circ} &= \angle OAC+35^{\circ} \\ \angle OAC &= 27,5^{\circ} \end{align} $
Sehingga,
$ \begin{align} &\angle OAC+\angle OBC+\angle ACB \\ &= 27,5^{\circ}+27,5^{\circ}+55^{\circ}\\ &= 110^{\circ} \end{align} $
Jadi pilihan jawaban yang BENAR adalah $(C) \ 110^{\circ} $.
Contoh Soal 10
Jika besar sudut $\angle \ BAC=35^{\circ}$, maka besar $\angle \ OBC=$ ...
$
\begin{align}
& (A) \ 50^{\circ} \\
& (B) \ 55^{\circ} \\
& (C) \ 60^{\circ} \\
& (D) \ 65^{\circ}
\end{align}
$
Jika besar sudut $\angle \ BAC=35^{\circ}$, maka besar $\angle \ OBC=$ ...
$
\begin{align}
\angle BOC &= 2 \times \angle BAC \\
&= 2 \times 35^{\circ} \\
&= 70^{\circ}
\end{align}
$
$ \begin{align} \angle OBC &= \left( \dfrac{180^{\circ}-\angle BOC}{2} \right) \\ &= \left( \dfrac{180^{\circ}-70^{\circ}}{2} \right) \\ &= 55^{\circ} \end{align} $
Jadi pilihan jawaban yang BENAR adalah $(B) \ 55^{\circ}$.
$ \begin{align} \angle OBC &= \left( \dfrac{180^{\circ}-\angle BOC}{2} \right) \\ &= \left( \dfrac{180^{\circ}-70^{\circ}}{2} \right) \\ &= 55^{\circ} \end{align} $
Jadi pilihan jawaban yang BENAR adalah $(B) \ 55^{\circ}$.
Penutup
Nah sahabat kreatif, bagaimana?Ternyata mencari sudut pusat dan sudut keliling pada lingkaran itu mudah bukan.
Perbanyak latihan dengan bentuk soal - soal yang lain agar kalian makin paham dan jago lagi.
Jangan lupa untuk share ke sahabat atau teman - teman jika pembahasan ini bermanfaat.
Selamat Belajar !
"Jika kamu bisa memimpikannya, kamu bisa melakukannya." – Walt Disney
