Cara Paling Cepat Dan Mudah Menghitung KPK Dan FPB Bilangan
Ini adalah pembahasan cara paling cepat dan mudah menghitung nilai KPK dan FPB suatu bilangan.
Hai adik - adik menghitung KPK dan FPB ternyata tidak sesusah yang dibayangkan lho.
Coba deh simak baik – baik pembahasan kita pada kesempatan kali ini bagi kalian yang masih sering kesulitan mengerjakan soal – soal tentang KPK dan FPB.
Namun sebelum kita bahas lebih lanjut cara cepat dan mudah untuk menghitung nilai KPK dan FPB , yuk kita awali dengan menelusuri sebenarnya apa itu KPK dan FPB.
KPK dari dua bilangan atau lebih adalah bilangan bulat positif terkecil yang dapat habis dibagi oleh bilangan – bilangan tersebut.
FPB dari dua bilangan atau lebih merupakan bilangan bulat positif terbesar yang dapat membagi habis bilangan – bilangan tersebut sekaligus.
Ada beberapa cara untuk Menghitung KPK Dan FPB Bilangan, dari yang paling panjang hingga terpendek atau tercepat.
Perhatikan baik – baik pembahasan kreatifmatematika.com di bawah ini.
Ikuti langkah – langkahnya ya adik – adik.
Dua cara tersebut adalah cara faktorisasi prima dan cara metriks (tabel).
Dengan menggunakan diagram pohon atau lebih kita kenal dengan pohon faktor maka akan kita peroleh,
Dari hasil menghitung KPK dan FPB dengan cara faktorisasi prima (pohon faktor) di atas bisa kita tulis sebagai berikut :
$16=2^{4}$
$30=2 \times 3 \times 5$
Dengan demikian maka FPB dari $16$ dan $30$ adalah ambil bilangan yang berada pada $16$ dan sekaligus juga di $30$ yaitu $2$.
Sedangkan KPK dari $16$ dan $30$ tinggal kalikan sisanya $2^{4} \times 3 \times 5$ yaitu $240$.
Karena dengan cara metriks kita akan jauh lebih mudah dan cepat menghitung nilai KPK dan FPB suatu bilangan.
Mengapa bisa lebih cepat dan mudah ?
Karena menghitung KPK dan FPB dengan cara metriks kita bisa susun bilangan - bilangan yang akan dihitung nilai KPK dan FPB nya dalam satu tabel sekaligus.
Jadi cara metriks menghitung nilai KPK dan FPB nya langsung jadi satu tanpa harus kita pisah - pisah seperti halnya menghitung dengan cara pohon faktor.
Kita akan kerjakan kembali soal yang sama seperti pada pembahasan di atas yaitu berapakah hasil KPK dan FPB dari 16 dan 30.
Catatan penting ketika memakai cara metriks adalah dengan melingkari bilangan yang bisa membagi habis keduanya.
Jika hanya bisa membagi salah satunya maka nilai yang satunya dibiarkan tetap.
Kita akan rangkai dua bilangan yang akan kita hitung nilai KPK dan FPB nya yaitu $16$ dan $30$ dalam satu tabel sekaligus.
Kemudian kita akan lakukan pembagian dengan menggunakan bilangan prima terkecil yang bisa membagi salah satu atau kedua bilangan tersebut.
Lebih detail lagi yuk perhatikan dengan baik tabel di bawah ini.
Terlihat jelas bukan dari tabel di atas bahwa hanya angka $2$ (yang dilingkari) yang bisa membagi habis keduanya.
Jadi dari hal tersebut dapat kita simpulkan bahwa nilai FPB dari $16$ dan $30$ adalah $2$.
Sedangkan angka pembagi sebelah kiri sisanya yaitu $2^{4} \times 3 \times 5$ merupakan nilai KPK nya.
Sehingga KPK dari $16$ dan $30$ adalah $2^{4} \times 3 \times 5=240$.
Kalau kita memakai cara faktorisasi prima tetap harus dibuat satu – satu pohon faktornya dari ketiga bilangan tersebut.
Nah biar lebih ringkas kita akan pakai cara metriks atau tabel, karena dengan cara ini mau tiga bilangan atau lebih semuanya tinggal di tata berdampingan dan langsung bisa dikerjakan sekaligus.
Ingat untuk selalu melingkari bilangan yang dapat membagi habis ketiga bilangan yang akan kita cari nilai KPK dan FPB nya.
Yuk langsung kita hitung nilai KPK dan FPB nya dengan menggunakan cara metriks atau tabel.
Sehingga,
Dengan demikian bisa kita simpulkan bahwa,
FPB dari $12$, $15$ dan $21$ adalah $3$.
KPK dari $12$, $15$ dan $21$ adalah $2^{2} \times 3 \times 5 \times 7=420$.
Sehingga,
Dengan demikian bisa kita simpulkan bahwa,
FPB dari $45$ dan $25$ adalah $5$.
KPK dari $45$ dan $25$ adalah $3^{2} \times 5^{2}=225$.
Sehingga,
Dengan demikian bisa kita simpulkan bahwa,
FPB dari $20$, $35$ dan $52$ adalah tidak ada.
KPK dari $20$, $35$ dan $52$ adalah $2^{2} \times 5 \times 7 \times 13=1.820$.
Yang paling penting di sini adalah kalian harus bisa cermati konteks cerita dari soal KPK dan FPB tersebut ya.
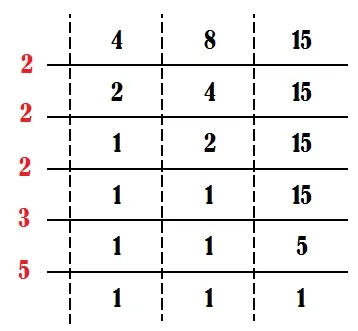
Untuk mengerjakan soal cerita di atas kita bisa hitung dengan menggunakan KPK dari $4$, $8$ dan $15$ untuk mengetahui kapan mereka bertiga akan latihan bersama lagi.
Sehingga,
KPK dari $4$, $8$ dan $15$ adalah $2^{3} \times 3 \times 5=120$.
Jadi dapat kita tarik kesimpulan bahwa mereka bertiga akan latihan bersama (bertemu) setiap $120$ hari sekali.
Jika mereka sudah pernah bertemu untuk latihan bersama pada tanggal $5$ Maret $2020$ maka mereka akan bertemu kembali pada :
$=$ $5$ Maret $2020$ $+$ $120$ hari $=$ $3$ Juli $2020$.
Semoga bisa membantu pemahaman kalian dalam belajar menghitung KPK dan FPB bilangan ya.
Coba deh simak baik – baik pembahasan kita pada kesempatan kali ini bagi kalian yang masih sering kesulitan mengerjakan soal – soal tentang KPK dan FPB.
Namun sebelum kita bahas lebih lanjut cara cepat dan mudah untuk menghitung nilai KPK dan FPB , yuk kita awali dengan menelusuri sebenarnya apa itu KPK dan FPB.
Apa itu KPK?
KPK adalah singkatan dari Kelipatan Persekutuan Terkecil.KPK dari dua bilangan atau lebih adalah bilangan bulat positif terkecil yang dapat habis dibagi oleh bilangan – bilangan tersebut.
Apa itu FPB?
Nah sedangkan FPB adalah singkatan dari Faktor Persekutuan Terbesar.FPB dari dua bilangan atau lebih merupakan bilangan bulat positif terbesar yang dapat membagi habis bilangan – bilangan tersebut sekaligus.
Ada beberapa cara untuk Menghitung KPK Dan FPB Bilangan, dari yang paling panjang hingga terpendek atau tercepat.
Perhatikan baik – baik pembahasan kreatifmatematika.com di bawah ini.
Ikuti langkah – langkahnya ya adik – adik.
Cara Mudah dan Cepat Menghitung KPK Dan FPB Bilangan
Ada dua cara yang cara yang paling mudah dan cepat yang bisa kita gunakan untuk menghitung nilai KPK dan FPB dari suatu bilangan.Dua cara tersebut adalah cara faktorisasi prima dan cara metriks (tabel).
1. Cara Faktorisasi Prima (Pohon Faktor)
Melalui faktorisasi prima kita akan mendapatkan bilangan prima berapa saja yang dapat membagi hasil dua bilangan atau lebih yang menjadi persoalan KPK dan FPB nya.
Contoh Soal Menghitung KPK dan FPB
Dengan cara faktorisasi prima atau pohon faktor nilai KPK dan FPB dari $16$ dan $30$ adalah...
Dengan cara faktorisasi prima atau pohon faktor nilai KPK dan FPB dari $16$ dan $30$ adalah...
Dengan menggunakan diagram pohon atau lebih kita kenal dengan pohon faktor maka akan kita peroleh,
$16=2^{4}$
$30=2 \times 3 \times 5$
Dengan demikian maka FPB dari $16$ dan $30$ adalah ambil bilangan yang berada pada $16$ dan sekaligus juga di $30$ yaitu $2$.
Sedangkan KPK dari $16$ dan $30$ tinggal kalikan sisanya $2^{4} \times 3 \times 5$ yaitu $240$.
2. Cara Metriks (Tabel)
Menghitung nilai KPK dan FPB menggunakan cara metriks atau tabel pada dasarnya bisa dikatakan sebagai cara penyempurnaan dari cara pohon faktor.Karena dengan cara metriks kita akan jauh lebih mudah dan cepat menghitung nilai KPK dan FPB suatu bilangan.
Mengapa bisa lebih cepat dan mudah ?
Karena menghitung KPK dan FPB dengan cara metriks kita bisa susun bilangan - bilangan yang akan dihitung nilai KPK dan FPB nya dalam satu tabel sekaligus.
Jadi cara metriks menghitung nilai KPK dan FPB nya langsung jadi satu tanpa harus kita pisah - pisah seperti halnya menghitung dengan cara pohon faktor.
Kita akan kerjakan kembali soal yang sama seperti pada pembahasan di atas yaitu berapakah hasil KPK dan FPB dari 16 dan 30.
Catatan penting ketika memakai cara metriks adalah dengan melingkari bilangan yang bisa membagi habis keduanya.
Jika hanya bisa membagi salah satunya maka nilai yang satunya dibiarkan tetap.
Contoh Soal Menghitung KPK dan FPB
Dengan cara metriks atau tabel nilai KPK dan FPB dari $16$ dan $30$ adalah...
Dengan cara metriks atau tabel nilai KPK dan FPB dari $16$ dan $30$ adalah...
Kita akan rangkai dua bilangan yang akan kita hitung nilai KPK dan FPB nya yaitu $16$ dan $30$ dalam satu tabel sekaligus.
Kemudian kita akan lakukan pembagian dengan menggunakan bilangan prima terkecil yang bisa membagi salah satu atau kedua bilangan tersebut.
Lebih detail lagi yuk perhatikan dengan baik tabel di bawah ini.
Jadi dari hal tersebut dapat kita simpulkan bahwa nilai FPB dari $16$ dan $30$ adalah $2$.
Sedangkan angka pembagi sebelah kiri sisanya yaitu $2^{4} \times 3 \times 5$ merupakan nilai KPK nya.
Sehingga KPK dari $16$ dan $30$ adalah $2^{4} \times 3 \times 5=240$.
Cara Mencari FPB dan KPK Tiga Bilangan
Mencari FPB dan KPK tiga bilangan sebenarnya tidak jauh berbeda dengan mencari KPK dan FPB dua bilangan.Kalau kita memakai cara faktorisasi prima tetap harus dibuat satu – satu pohon faktornya dari ketiga bilangan tersebut.
Nah biar lebih ringkas kita akan pakai cara metriks atau tabel, karena dengan cara ini mau tiga bilangan atau lebih semuanya tinggal di tata berdampingan dan langsung bisa dikerjakan sekaligus.
Ingat untuk selalu melingkari bilangan yang dapat membagi habis ketiga bilangan yang akan kita cari nilai KPK dan FPB nya.
Contoh Soal Menghitung KPK dan FPB
Nilai KPK dan FPB dari $12$, $15$ dan $21$ adalah...
Nilai KPK dan FPB dari $12$, $15$ dan $21$ adalah...
Yuk langsung kita hitung nilai KPK dan FPB nya dengan menggunakan cara metriks atau tabel.
Sehingga,
Dengan demikian bisa kita simpulkan bahwa,
FPB dari $12$, $15$ dan $21$ adalah $3$.
KPK dari $12$, $15$ dan $21$ adalah $2^{2} \times 3 \times 5 \times 7=420$.
Soal dan Pembahasan KPK dan FPB
Soal 1. Menghitung KPK dan FPB
Nilai KPK dan FPB dari $45$ dan $25$ adalah...
Nilai KPK dan FPB dari $45$ dan $25$ adalah...
Sehingga,
FPB dari $45$ dan $25$ adalah $5$.
KPK dari $45$ dan $25$ adalah $3^{2} \times 5^{2}=225$.
Soal 2. Menghitung KPK dan FPB
Nilai KPK dan FPB dari $20$, $35$ dan $52$ adalah...
Nilai KPK dan FPB dari $20$, $35$ dan $52$ adalah...
Sehingga,
FPB dari $20$, $35$ dan $52$ adalah tidak ada.
KPK dari $20$, $35$ dan $52$ adalah $2^{2} \times 5 \times 7 \times 13=1.820$.
Soal Cerita KPK dan FPB
Adakalanya memang contoh soal KPK dan FPB dalam bentuk soal cerita.Yang paling penting di sini adalah kalian harus bisa cermati konteks cerita dari soal KPK dan FPB tersebut ya.
Soal Cerita Menghitung KPK dan FPB
Adi adalah seorang atlit renang, ia rajin berlatih setiap $4$ hari sekali. Banu memang tidak pandai renang namun dia setiap $8$ hari sekali selalu menyempatkan diri untuk berlatih fitnes. Berbeda dengan kedua sahabatnya, Rani sangat menyukai menari. Rani belum pernah absen dari jadwal latihan tarinya tiap $15$ hari sekali. Jika mereka bertiga sudah pernah bertemu untuk latihan bersama tanggal $5$ Maret $2020$ maka pada tanggal berapakah ketiga sahabat tersebut akan bertemu ditempat latihan jika ketiganya memiliki tempat latihan SPORT CENTRE yang sama ?
Adi adalah seorang atlit renang, ia rajin berlatih setiap $4$ hari sekali. Banu memang tidak pandai renang namun dia setiap $8$ hari sekali selalu menyempatkan diri untuk berlatih fitnes. Berbeda dengan kedua sahabatnya, Rani sangat menyukai menari. Rani belum pernah absen dari jadwal latihan tarinya tiap $15$ hari sekali. Jika mereka bertiga sudah pernah bertemu untuk latihan bersama tanggal $5$ Maret $2020$ maka pada tanggal berapakah ketiga sahabat tersebut akan bertemu ditempat latihan jika ketiganya memiliki tempat latihan SPORT CENTRE yang sama ?
Untuk mengerjakan soal cerita di atas kita bisa hitung dengan menggunakan KPK dari $4$, $8$ dan $15$ untuk mengetahui kapan mereka bertiga akan latihan bersama lagi.
Sehingga,
Jadi dapat kita tarik kesimpulan bahwa mereka bertiga akan latihan bersama (bertemu) setiap $120$ hari sekali.
Jika mereka sudah pernah bertemu untuk latihan bersama pada tanggal $5$ Maret $2020$ maka mereka akan bertemu kembali pada :
$=$ $5$ Maret $2020$ $+$ $120$ hari $=$ $3$ Juli $2020$.
Penutup
Nah adik - adik itu pembahasan kita kali ini tentang cara paling mudah dan cepat untuk menghitung nilai KPK dan FBP dari suatu bilangan.Semoga bisa membantu pemahaman kalian dalam belajar menghitung KPK dan FPB bilangan ya.
Jangan lupa untuk share ke sahabat atau teman - teman jika pembahasan ini bermanfaat.
Selamat Belajar !
“Hiduplah seolah engkau mati besok. Belajarlah seolah engkau hidup selamanya.” – Mahatma Gandhi
