Rangkuman Materi Lingkaran Lengkap
Ini adalah rangkuman lengkap materi lingkaran yang disertai contoh - contoh soal latihan dan pembahasannya.
Daftar Isi
PENGERTIAN LINGKARAN
Lingkaran $\to$ bentuk yang terdiri dari semua titik dalam bidang yang berjarak tertentu dari titik tertentu, pusat; ekuivalennya adalah kurva yang dilacak oleh titik yang bergerak dalam bidang sehingga jaraknya dari titik tertentu adalah konstan. Jarak antara titik mana pun dari lingkaran dan pusat disebut jari-jari.
Beberapa bagian lingkaran yang perlu kalian ketahui adalah :
- Titik pusat : merupakan titik tengah lingkaran, di mana jarak titik tersebut dengan titik manapun pada lingkaran selalu tetap.
- Jari-jari atau radius : merupakan garis lurus yang menghubungkan titik pusat dengan lingkaran.
- Tali busur : merupakan garis lurus di dalam lingkaran yang memotong lingkaran pada dua titik yang berbeda.
- Busur : merupakan garis lengkung baik terbuka, maupun tertutup yang berimpit dengan lingkaran.
- Keliling lingkaran : merupakan busur terpanjang pada lingkaran.
- Diameter : merupakan tali busur terbesar yang panjangnya adalah dua kali dari jari-jarinya. Diameter ini membagi lingkaran sama luas.
- Apotema : merupakan garis terpendek antara tali busur dan pusat lingkaran.
- Juring: merupakan daerah pada lingkaran yang dibatasi oleh busur dan dua buah jari-jari yang berada pada kedua ujungnya.
- Tembereng : merupakan daerah pada lingkaran yang dibatasi oleh sebuah busur dengan tali busurnya.
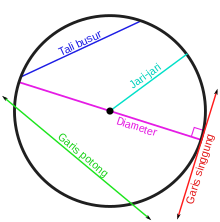 |
| Tali busur, garis potong, garis singgung, jari-jari, dan diameter. |
 |
| Busur, juring, dan tembereng |
Gambar disunting dari : Wikipedia
PERSAMAAN LINGKARAN
- Persamaan lingkaran yang berpusat di $P(a,b)$ :$(x-a)^{2}+(y-b)^{2}=r^{2}$
- Persamaan lingkaran yang berpusat di $O(0,0)$ :$x^{2}+y^{2}=r^{2}$
- Jarak Titik $(x_1, y_1)$ Terhadap Titik $(x_2, y_2)$ : $d=\sqrt{(x_2-x_1)^{2}+(y_2-y_1)^{2}}$
- Jarak Titik $(x_1, y_1)$ Terhadap Garis $Ax+By+C=0$ : $d=\left| \dfrac{Ax_1+By_1+C}{\sqrt{A^{2}+B^{2}}} \right|$
BENTUK UMUM PERSAMAAN LINGKARAN
$x^{2}+y^{2}+Ax+By+C=0$
dimana koordinat pusat :
$P(-\dfrac{1}{2}a,-\dfrac{1}{2}b)$
serta jari - jari :
$r=\sqrt{\dfrac{1}{4}A^{2}+\dfrac{1}{4}B^{2}-C}$
PERSAMAAN GARIS SINGGUNG LINGKARAN
1. Persamaan Garis Singgung Lingkaran Melalui $(x_1, y_1)$ :
- $P(0,0) \to x_1 \cdot x+y_1 \cdot y=r^{2}$
- $P(a,b) \to (x_1-a)(x-a)+(y_1-b)(y-b)=r^{2}$
2. Persamaan Garis Singgung Lingkaran Bergradien $(m)$ :
- $P(0,0) \to y=mx \pm r\sqrt{m^{2}+1}$
- $P(a,b) \to y-b=m(x-a) \pm r\sqrt{m^{2}+1}$
CONTOH SOAL LATIHAN DAN PEMBAHASAN MATERI LINGKARAN LENGKAP
1. Persamaan lingkaran yang berpusat di $O(0,0)$ dan mempunyai jari - jari $3$ adalah...
$\begin{align} (A)\ & x^{2}+y^{2}=3 \\ (B)\ & x^{2}+y^{2}=6 \\ (C)\ & x^{2}+y^{2}=9 \\ (D)\ & x^{2}+y^{2}=\sqrt{3} \\ (E)\ & x^{2}+y^{2}=\sqrt{6} \end{align}$
Pembahasan :
$\begin{align} x^{2}+y^{2} & =r^{2} \\ x^{2}+y^{2}& =3^{2} \\ x^{2}+y^{2}& =9 \end{align}$
Jadi pilihan jawaban yang benar adalah (C) $x^{2}+y^{2}=9$
2. Persamaan lingkaran yang berpusat di $A(2,3)$ dan berjari - jari $5$ adalah...
$\begin{align} (A)\ & (x+2)^{2}+(y-3)^{2}=25 \\ (B)\ & (x-2)^{2}+(y+3)^{2}=25 \\ (C)\ & (x+2)^{2}+(y+3)^{2}=25 \\ (D)\ & (x-2)^{2}+(y-3)^{2}=25 \\ (E)\ & (x-2)^{2}-(y-3)^{2}=25 \end{align}$
Pembahasan :
$\begin{align} (x-a)^{2}+(y-b)^{2} & = r^{2} \\ (x-2)^{2}+(y-3)^{2} & = 5^{2} \\ (x-2)^{2}+(y-3)^{2} & = 25 \end{align}$
Jadi pilihan jawaban yang benar adalah (D) $(x-2)^{2}+(y-3)^{2}=25$
3. Bentuk persamaan lingkaran yang mempunyai pusat $P(1,6)$ dan berjari - jari $4$ adalah...
$\begin{align} (A)\ & x^{2}+y^{2}+2x-12y+21=0 \\ (B)\ & x^{2}+y^{2}-2x+12y+21=0 \\ (C)\ & x^{2}+y^{2}-2x-12y+21=0 \\ (D)\ & x^{2}+y^{2}-12x-2y+21=0 \\ (E)\ & x^{2}+y^{2}+2x+12y+21=0 \end{align}$
Pembahasan :
$\begin{align} (x-a)^{2}+(y-b)^{2} & = r^{2} \\ (x-1)^{2}+(y-6)^{2} & = 4^{2} \\ x^{2}-2x+1+y^{2}-12y+36 & = 16 \\ x^{2}-2x+1+y^{2}-12y+36 & = 16 \\ x^{2}+y^{2}-2x-12y+37 - 16 & = 0 \\ x^{2}+y^{2}-2x-12y+21 & = 0 \end{align}$
Jadi pilihan jawaban yang benar adalah (C) $x^{2}+y^{2}-2x-12y+21 = 0$
TRIK SUPERKILAT!!!
Lingkaran pusat $P( \color{red}{a}, \color{red}{b})$ dan jari - jari $\color{blue}{r}$ maka persamaan lingkarannya adalah :
$x^{2}+y^{2}+\color{red}{a}(-2)x+\color{red}{b}(-2)y+(\color{red}{a^{2}}+\color{red}{b^{2}}-\color{blue}{r^{2}})=0$
Lingkaran pusat $P(\color{red}{1},\color{red}{6})$ dan $r=\color{blue}{4}$ maka persamaan lingkarannya adalah :
$\begin{align} x^{2}+y^{2}+ \color{red}{1}(-2)x+ \color{red}{6}(-2)y+( \color{red}{1^{2}}+ \color{red}{6^{2}}-\color{blue}{4^{2}}) & =0 \\ x^{2}+y^{2}-2x-12y+21 & = 0 \end{align}$
4. Persamaan lingkaran yang berpusat di $O(0,0)$ dan melalui titik $A(6,-8)$ adalah...
$\begin{align} (A)\ & x^{2}+y^{2}=10 \\ (B)\ & x^{2}+y^{2}=100 \\ (C)\ & x^{2}+y^{2}=\sqrt{10} \\ (D)\ & x^{2}+y^{2}=5 \\ (E)\ & x^{2}+y^{2}=25 \end{align}$
Pembahasan :
Untuk mengerjakan soal di atas kita butuh rumus jarak titik terhadap titik yaitu :
- $d=\sqrt{(x_2-x_1)^{2}+(y_2-y_1)^{2}}$
Sehingga kita akan peroleh nilai jari - jari :
$\begin{align} r & =\sqrt{(6-0)^{2}+(-8-0)^{2}} \\ & = \sqrt{36+64} \\ & = \sqrt{100} \\ & = 10 \end{align}$
Dengan demikian kita akan peroleh,
$\begin{align} x^{2}+y^{2} & =r^{2} \\ x^{2}+y^{2}& =10^{2} \\ x^{2}+y^{2}& =100 \end{align}$
Jadi pilihan jawaban yang benar adalah (B) $x^{2}+y^{2}=100$
5. Persamaan lingkaran yang berpusat di $P(3,-7)$ dan menyinggung sumbu-$x$ adalah...$\begin{align} (A)\ & x^{2}+y^{2}-6x+14y+9=0 \\ (B)\ & x^{2}+y^{2}+6x+14y+9=0 \\ (C)\ & x^{2}+y^{2}-3x-14y+9=0 \\ (D)\ & x^{2}+y^{2}+6x-14y-9=0 \\ (E)\ & x^{2}+y^{2}-6x+7y+9=0 \end{align}$
Pembahasan :
TRIK SUPERKILAT !!!
Lingkaran berpusat di $P(a,b)$ meyinggung sumbu-$x$ $\to$ $r=|b|$
Oleh karena itu yang dimaksud soal di atas adalah persamaan lingkaran yang berpusat di $P(3,-7)$ dan berjari - jari $|-7|=7$, sehingga
$\begin{align} (x-a)^{2}+(y-b)^{2} & = r^{2} \\ (x-3)^{2}+(y+7)^{2} & = 7^{2} \\ x^{2}-6x+9+y^{2}+14y+49 & = 49 \\ x^{2}+y^{2}-6x+14y+9 & = 0 \end{align}$
Jadi pilihan jawaban yang benar adalah (A) $x^{2}+y^{2}-6x+14y+9=0$
6. Persamaan lingkaran yang berpusat di $P(-5,2)$ dan menyinggung sumbu-$y$ adalah...
$\begin{align} (A)\ & x^{2}+y^{2}-5x-4y+4=0 \\ (B)\ & x^{2}+y^{2}+10x-2y+4=0 \\ (C)\ & x^{2}+y^{2}+10x-4y+4=0 \\ (D)\ & x^{2}+y^{2}+10x+4y+14=0 \\ (E)\ & x^{2}+y^{2}+5x-2y+4=0 \end{align}$
Pembahasan :
TRIK SUPERKILAT !!!
Lingkaran berpusat di $P(a,b)$ meyinggung sumbu-$y$ $\to$ $r=|a|$
Dengan demikian kita akan dapatkan nilai dari jari - jari lingkaran yang dimaksud, yaitu :
$\begin{align} r & = |-5| \\ & = 5 \end{align}$
Sehingga persamaan lingkaran yang berpusat di $P(-5,2)$ dan $r=5$ ialah :
$\begin{align} (x-a)^{2}+(y-b)^{2} & = r^{2} \\ (x+5)^{2}+(y-2)^{2} & = 5^{2} \\ x^{2}+10x+25+y^{2}-4y+4 & = 25 \\ x^{2}+y^{2}+10x-4y+4 & = 0 \end{align}$
Jadi pilihan jawaban yang benar adalah (C) $x^{2}+y^{2}+10x-4y+4=0$
7. Jika persamaan lingkaran yang berpusat di $P(a,-8)$ dan berjari - jari $3$ adalah $x^{2}+y^{2}-10x+16y+80=0$, maka nilai dari $a$ adalah...
$\begin{align} (A)\ & 1 \\ (B)\ & 2 \\ (C)\ & 3 \\ (D)\ & 4 \\ (E)\ & 5 \end{align}$
Pembahasan :
Untuk mengerjakan soal di atas kita butuh rumus untuk mencari pusat jika diketahui bentuk umum dari persamaan lingkaran :
$x^{2}+y^{2}+Ax+By+C=0$ $\to$ $P(-\dfrac{1}{2}a,-\dfrac{1}{2}b)$
Sehingga,
$\begin{align} a & =-\dfrac{1}{2} \cdot (-10) \\ a & = 5 \end{align}$
Jadi pilihan jawaban yang benar adalah (E) $5$
8. Jika $x_1$ dan $x_2$ merupakan akar - akar dari persamaan kuadrat $x^{2}-2x+3=0$, maka persamaan lingkaran yang berpusat di $P(x_1+x_2, x_1x_2)$ dan berjari - jari $(x_1+x_2+1)$ adalah...
$\begin{align} (A)\ & x^{2}+y^{2}-4x-6y+4=0 \\ (B)\ & x^{2}+y^{2}+4x+6y+4=0 \\ (C)\ & x^{2}+y^{2}-2x-3y+4=0 \\ (D)\ & x^{2}+y^{2}+2x+3y+4=0 \\ (E)\ & x^{2}+y^{2}-4x+3y+4=0 \end{align}$
Pembahasan :
Rumus Operasi Akar dalam persamaan kuadrat akan dibutuhkan untuk menyelesaikan soal di atas :
$\begin{align} ax^{2}+bx+c & = 0 \\ x_1+x_2 & = -\dfrac{b}{a} \\ x_1x_2 & = \dfrac{c}{a} \end{align}$
Dari persamaan kuadrat yang ada di soal kita akan peroleh
$\begin{align} x^{2}-2x+3 & = 0 \\ \to x_1+x_2 & = 2 \\ \to x_1x_2 & = 3 \end{align}$
Dengan demikian pusat dan jari - jari lingkaran yang ditanyakan adalah $P(2,3)$ dan $r=3$
Dengan memakai TRIK SUPERKILAT!!! kita akan dapatkan persamaan lingkarannya adalah :
$\begin{align} x^{2}+y^{2}+2(-2)x+3(-2)y+(2^{2}+3^{2}-3^{2}) & =0 \\ x^{2}+y^{2}-4x-6y+4 & = 0 \end{align}$
Jadi pilihan jawaban yang benar adalah (A) $x^{2}+y^{2}-4x-6y+4=0$
9. Persamaan lingkaran yang berpusat di $P(3,-4)$ dan melalui $Q(6,0)$ adalah...Pembahasan :
Dari soal dapat kita ketahui bahwa jari - jari dari lingkaran tersebut adalah jarak dari titik $P$ ke $Q$.
Sehingga,
$\begin{align} r & = \sqrt{(6-3)^{2}+(0-(-4))^{2}} \\ & = \sqrt{9+16} \\ & = \sqrt{25} \\ & = 5 \end{align}$
$\begin{align} (x-a)^{2}+(y-b)^{2} & = r^{2} \\ (x-3)^{2}+(y+4)^{2} & = 5^{2} \\ x^{2}-6x+9+y^{2}+8y+16 & = 25 \\ x^{2}+y^{2}-6x+8y & = 0 \end{align}$
Jadi pilihan jawaban yang tepat adalah (A) $x^{2}+y^{2}-6x+8y=0$
10. Persamaan lingkaran yang berpusat di $P(-1,5)$ dan menyinggung garis $3x+4y-7=0$ adalah...
$\begin{align} (A)\ & x^{2}+y^{2}+5x-y+22=0 \\ (B)\ & x^{2}+y^{2}+x-5y+22=0 \\ (C)\ & x^{2}+y^{2}+2x-10y+20=0 \\ (D)\ & x^{2}+y^{2}+2x-10y+22=0 \\ (E)\ & x^{2}+y^{2}+2x-10y=0 \end{align}$
Pembahasan :
Untuk mengerjakan soal di atas kita butuh rumus mencari jarak titik $(x_1, y_1)$ terhadap garis $Ax+By+C=0$ :
$d=\left| \dfrac{Ax_1+By_1+C}{\sqrt{A^{2}+B^{2}}} \right|$
Dengan demikian,
$\begin{align} r & = \left| \dfrac{3(-1)+4(5)-7}{\sqrt{3^{2}+4^{2}}} \right| \\ & = \left| \dfrac{-3+20-7}{\sqrt{25}} \right| \\ & = \left| \dfrac{10}{5} \right| \\ & = 2 \end{align}$
TRIK SUPERKILAT!!!
Lingkaran berpusat di $P(-1,5)$ dan $r=2$ adalah :
$\begin{align} x^{2}+y^{2}+(-1)(-2)x+5(-2)y+((-1)^{2}+5^{2}-2^{2}) & =0 \\ x^{2}+y^{2}+2x-10y+22 & = 0 \end{align}$
Jadi pilihan jawaban yang benar adalah (D) $x^{2}+y^{2}+2x-10y+22=0$
Penutup
Nah sahabat kreatif, itu lah pembahasan Rangkuman Materi Lingkaran Lengkap.
Jangan lupa untuk share ke sahabat atau teman - teman jika pembahasan ini bermanfaat.
Selamat Belajar !


